Duration: Een maatstaf voor de rentegevoeligheid van een obligatie.

Duration is een belangrijk concept binnen de wereld van vastrentende beleggingen. Het is een maatstaf die aangeeft hoe gevoelig een obligatie is voor veranderingen in de rente.

Om het concept van duration uit te leggen, is het handig om eerst wat basisbegrippen te definiëren. Een obligatie is in feite een lening die wordt verstrekt door een uitgever (bijvoorbeeld een bedrijf of overheid) aan een obligatiehouder. De obligatiehouder ontvangt periodiek rentebetalingen en krijgt aan het einde van de looptijd van de obligatie zijn inleg terug. De rente die wordt betaald op de obligatie is vastgelegd bij uitgifte en wordt meestal uitgedrukt als een percentage van de nominale waarde van de obligatie.

De rente die wordt betaald op de obligatie is echter niet altijd gelijk aan de marktrente. Als de marktrente stijgt, kan de rente op de obligatie relatief laag lijken en omgekeerd. Dit kan invloed hebben op de waarde van de obligatie op de secundaire markt.

De duration van een obligatie is een maatstaf voor de gemiddelde looptijd van de kasstromen van de obligatie. Met andere woorden, het geeft aan hoe lang het duurt voordat een obligatiehouder zijn inleg terugverdient via de couponbetalingen en de aflossing van de obligatie.

Wanneer de rente stijgt, heeft dit een negatief effect op de waarde van een obligatie. De reden hiervoor is dat nieuwe obligaties worden uitgegeven met een hogere rente, waardoor de oudere obligaties minder aantrekkelijk worden voor beleggers. Hoe langer de duration van de obligatie, hoe gevoeliger de waarde van de obligatie is voor veranderingen in de rente. Dit komt doordat de kasstromen van de obligatie verder in de toekomst liggen en dus meer worden beïnvloed door veranderingen in de marktrente.

Stel bijvoorbeeld dat een belegger een obligatie heeft met een duration van 5 jaar. Als de marktrente met 1% stijgt, zal de waarde van de obligatie naar verwachting met ongeveer 5% dalen. Als de duration 10 jaar is, zal de waarde van de obligatie naar verwachting met ongeveer 10% dalen bij een stijging van 1% in de marktrente.

Kortom, duration is een belangrijk concept voor beleggers die willen begrijpen hoe gevoelig hun vastrentende beleggingen zijn voor veranderingen in de rente. Het geeft inzicht in de gemiddelde looptijd van de kasstromen van de obligatie en kan helpen bij het bepalen van de juiste balans tussen risico en rendement in een vastrentende portefeuille.

Berekening

De koers van een obligatie is gevoelig voor vier factoren, met name de looptijd, aflossing en couponbetalingen en het interestniveau (c.q. rente). Dit vindt men ook terug in de wiskundige formule voor de duration.

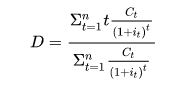
D = Duration;
C = Cashflow;
i = Discontovoet (marktrente of effectief rendement, niet de couponrente)
t = Tijd;
n = Looptijd.

In feite is het de gewogen gemiddelde looptijd van alle cashflows (coupons en aflossing van de hoofdsom) van een obligatie, waarbij het gewicht van elke kasstroom wordt bepaald door het relatieve belang van die kasstroom. Bij een obligatie met een looptijd van 10 jaar kan de duration (afhankelijk van de coupon en het rendement) bijvoorbeeld 7 jaar zijn. Als je de wiskundige formule van dichtbij bekijkt zie je dat de duration voor een obligatie zonder coupon, ook wel ‘zero coupon bond’, gelijk is aan de looptijd ervan. Neem je bijvoorbeeld een ‘zero’ met een looptijd van 10 jaar, dan rest slechts een cashflow (C) over 10 jaar en is de terugverdientijd of duration (D) precies die 10 jaar (n). Naarmate de couponbetalingen groter zijn (couponrente hoger), neemt de duration (en het koersrisico) af.

Modified Duration

Een afgeleide van de duration is de modified duration: hierbij wordt de duration gedeeld door (1+yield to maturity). Een obligatie met een duration van 8 jaar heeft bij een rendement van 5% een modified duration van 7.6 jaar.

Het nut hiervan is dat hiermee (behoorlijk) exact berekend kan worden wat de effecten zijn van een verandering in de marktrente, en daarmee van het rendement van de lening. Indien de marktrente met 1%-punt stijgt, zal de koers van de obligatie dalen met de modified duration (7.6% in dit voorbeeld) maal de oorspronkelijke koers van de obligatie. Als de oorspronkelijke koers 105% was bij een rendement van 5%, zal de koers bij een marktrente van 6% dalen tot (bij benadering) 105% – (7.6 x 1.05) = 105% – 7.98% = 97.02%.

Als vuistregel kan worden aangehouden: stijgt of daalt de rente met 1%, dan fluctueert de waarde van de obligatie met 1% maal de duration.

Hoewel duration (en modified duration) plegen te worden uitgedrukt in jaren, is het theoretisch niet geheel juist om dit als een tijdsperiode te zien. Het is een gevoeligheidsindicator. De verhouding tussen de relatieve verandering van de koers, dK/K, en de yieldverandering in %-punten, di. Dit kan worden aangetoond met behulp van de wiskundige differentiatie-techniek: (dK/K)/di = (dK/di)/K. Waarbij K de Contante Waarde (c.q. koers) voorstelt. De d is de wiskundige notatie voor een (ultrakleine) verandering.

Een praktijk voorbeeld

In 2022 zijn de rentes sterk gestegen. Hieronder hebben we de koersontwikkeling van twee obligatie ETF’s weergegeven. Links de iShares € Govt Bond 3-7yr UCITS ETF (EUR) met een duration van 4,59 en rechts de iShares € Govt Bond 15-30yr UCITS ETF (EUR) met een duration van 16.18.

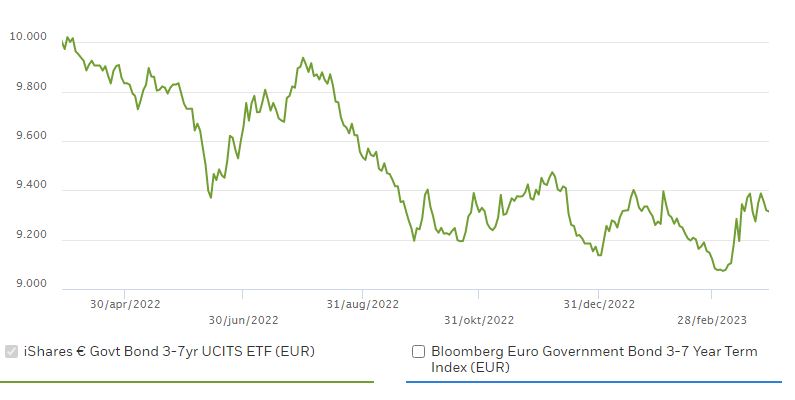
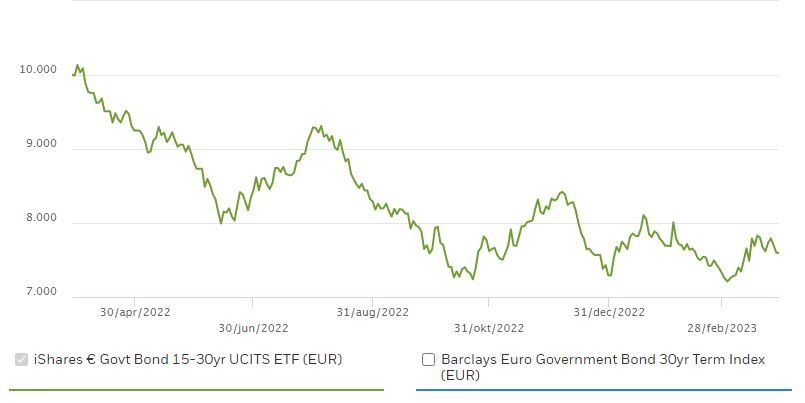
De obligatie ETF met de korte duration verloor 6,81% in waarde. De obligatie met een lange duration verloor 24,04 in waarde.

Conclusie

De duration is een belangrijke maatstaf voor het bepalen van het rente-risico.